
“Mathematics is not about numbers, equations, computations or algorithms;
It is about understanding” —William Paul Thurston.
The Department of Mathematics has been an integral part of Sukanta Mahavidyalaya since 1995-1996. Presently this Department has eighty (80) students pursuing their path towards a glorious career. The Department has five (05) dedicated faculty members who are caring for the students at this time.
In recent past, after obtaining bachelor degree (Honours ) in Mathematics from this institution, Sukanta Mahavidyalaya, Dhupguri, Jalpaiguri, many students admitted themselves for postgraduate study in mathematics at IIT Madras, IIT Kanpur, IIT Bhubaneswar, Hyderabad Central University, NIT Warangal, NIT Durgapur, the University of North Bengal, Panchanan Barma University etc. and many students are pursuing Ph.D. programme in mathematics at NIT Silchar, the University of North Bengal etc. Additionally, a good number of students from this department are performing their Job in various State and Central Government departments.
This Department shares a good quality computer laboratory with the Computer Science Department of this College and is planning for a new laboratory of its own.
A quality higher education must enable personal performance and knowledge, constructive and productive contribution to the society. For this, the Department of Mathematics always tries to make good quality education among the students through a combination of continuous internal evaluation, internal seminar, smart classes, virtual classes and sustenance dedicated initiatives. And try to perform among the students on the basis of curricular perspective, teaching-learning and evaluation, investigation for excellence, student support, progression, institutional values and best practices. Apart from these, students are provided good quality higher education and career counselling service for the future in a regular manner.

Assistant Professor
View Profile
Assistant Professor
View Profile
Assistant Professor
View Profile
State Aided College Teacher
View Profile
State Aided College Teacher
View ProfileNOTICE
Department of Mathematics
DATE |
SUBJECT |
|---|---|
20th February, 2024 |
NOTICE FOR SPECIAL LECTURE ON 'DYNAMICAL MODELLING FOR SYSTEMS BIOLOGY' |
3rd March, 2023 |
NOTICE REGARDING 4TH & 6TH SEMESTER INTERNAL EXAM. |
24th January, 2023 |
NOTICE REGARDING 1ST SEMESTER INTERNAL EXAM. |
3rd December, 2022 |
NOTICE FOR 5th SEMESTER HONOURS PRACTICAL EXAM |
29th November, 2022 |
NOTICE FOR INTERNAL EXAMINATIONS OF 1ST SEMESTER |
21st November, 2022 |
NOTICE FOR INTERNAL EXAMINATIONS OF 3RD SEMESTER GE |
14th November, 2022 |
NOTICE FOR INTERNAL EXAMINATIONS OF 3RD AND 5TH SEMESTER |
14th November, 2022 |
NOTICE FOR SPECIAL LECTURE ON 'NECESSITY & IMPORTANCE OF NUMERICAL ANALYSIS' |
12th September, 2022 |
NOTICE FOR INTERNAL EXAMINATIONS OF 3RD AND 5TH SEMESTER |
10th September, 2022 |
ACADEMIC CALENDER |
3rd February, 2022 |
NOTICE FOR PRACTICAL EXAMINATION |
18th February, 2021 |
NOTICE FOR PRACTICAL EXAMINATION |
Course Offered: This Department offers
SYLLABUS
Department of Mathematics
| FYUGP SYLLABUS (W.E.F.-25.07.2023) |
|---|
| REVISED CBCS SYLLABUS (W.E.F.-02.01.2023) |
| CBCS SYLLABUS (INTRODUCED IN 2018) |
Programme Outcome (Honours)
1. Develop critical thinking to gain scientific temper
2. Enrich the capability of problem solving
3. Enhance the correlation with the other science subjects
4. Able to apply the practical skills and technical knowledge
5. Making more eligible for employability
Programme Outcome (Programme Course)
1. Develop critical thinking to gain scientific temper
2. Enrich the capability of problem solving
3. Enhance the correlation with the other science subjects
4. Able to apply the practical skills and technical knowledge
5. Making more eligible for employability
COURSE OUTCOME
COURSE OUTCOME (HONOURS)
MTMH-HCC-I(Semester 1)
Eligible for finding Arc length of a curve, area of the region bounded by a given curve, Surface area and Volume of revolution by a curve about a given axis, techniques of sketching conics.
Eligible for derivation of reduction formulae of some special functions.
Eligible for calculating, application of Leibnitz rule and L’Hospital’s rule in business, economics and life sciences.
Eligible in various concepts and applications of two and three dimensions geometry.
Eligible for acquiring the knowledge about differential equations and its real life application.
MTMH-HCC-II(Semester 1)
Students will be able to calculate nth roots of unity and apply D’Moivre’s theorem.
Students will acquire knowledge on the theory of equations and its applications.
Students will be able to solve various inequalities and apply them to different problems.
Students will have a clear concept on functions, relations, well-ordering principle, division algorithm, principle of induction and their applications.
Students will be able to determine the rank of a matrix and its application on solving systems of linear equations.
Students will acquire knowledge on eigen values and eigen vectors.
Students will be acquainted with linear transformations and related problems.
MTMH-HCC-I(Semester 1)
Eligible for finding Arc length of a curve, area of the region bounded by a given curve, Surface area and Volume of revolution by a curve about a given axis, techniques of sketching conics.
Eligible for derivation of reduction formulae of some special functions.
Eligible for calculating, application of Leibnitz rule and L’Hospital’s rule in business, economics and life sciences.
Eligible in various concepts and applications of two and three dimensions geometry.
Eligible for acquiring the knowledge about differential equations and its real life application.
MTMH-HCC-II(Semester 1)
Students will be able to calculate nth roots of unity and apply D’Moivre’s theorem.
Students will acquire knowledge on the theory of equations and its applications.
Students will be able to solve various inequalities and apply them to different problems.
Students will have a clear concept on functions, relations, well-ordering principle, division algorithm, principle of induction and their applications.
Students will be able to determine the rank of a matrix and its application on solving systems of linear equations.
Students will acquire knowledge on eigen values and eigen vectors.
Students will be acquainted with linear transformations and related problems.
GE : Geometry, Calculus and Differential Equations (Semester 1)
Eligible for finding Arc length of a curve, area of the region bounded by a given curve, Surface area and Volume of revolution by a curve about a given axis, techniques of sketching conics
Eligible for derivation of reduction formulae of some special functions
Eligible for calculating, application of Leibnitz rule and L’Hospital’s rule in business, economics and life sciences.
Eligible in various concepts and applications of two and three dimensions geometry.
Eligible for acquiring the knowledge about differential equations and its real life application.
MTMH-HCC-III(Semester 2)
Students will gather an elaborate knowledge on real number systems with special emphasis on completeness property of R, Archimedean property, density of rational numbers in R, Bolzano-Weierstrass theorem, Heine-Borel theorem.
Students will be able to understand the sequence of real numbers and its different properties.
Skill of determining convergence of infinite series of real numbers will be developed.
MTMH-HCC-IV(Semester 2)
Students will acquire knowledge on solving linear homogeneous and non-homogeneous equations of higher order with constant co-efficient, Wronskian, method of undetermined co-efficient, method of variation of parameters.
Students will learn basic theory of linear systems in normal form, two equations in two unknown functions.
Students will be able to solve the power series solution of a differential equation about an ordinary and regular singular point.
Students will gather knowledge on how to apply vector triple product, vector calculus and vector integration.
GE : Algebra (Semester 2)
Students will be able to calculate nth roots of unity and apply D’Moivre’s theorem.
Students will acquire knowledge on the theory of equations and its applications.
Students will be able to solve various inequalities and apply them to different problems.
Students will have a clear concept on functions, relations, well-ordering principle, division algorithm, principle of induction and their applications.
Students will be able to determine the rank of a matrix and its application on solving systems of linear equations.
Students will acquire knowledge on eigen values and eigen vectors.
Students will be acquainted with linear transformations and related problems.
MTMH-HCC-V (Semester 3)
Students will learn the concepts of limit and continuity of real functions.
Students will acquire knowledge on differentiability of functions in R and application of Rolle’s theorem, Mean value theorem, Intermediate value property of derivatives, Darboux theorem.
Students will be able to derive Taylor’s series and Maclaurin’s series expansion of some functions.
Students will be able to explore concepts of metric spaces.
MTMH-HCC-VI (Semester 3)
Students will be able to define group and can give examples of groups, especially permutation group, symmetries of a square, dihedral group, quaternion group.
Students will also learn different elementary properties of group theory.
Students will be able to describe subgroup, cyclic group, cosets, normal subgroup, quotient group and homomorphism of groups with special emphasis on first, second and third isomorphism theorems.
MTMH-HCC-VII (Semester 3)
Students will acquire a very clear knowledge on Riemann Integrations
Students will be able to solve different types of improper integrals and their convergences.
Students will learn sequence and series of functions.
Students will be able to solve different Fourier series and Power series.
SEC-1 LOGIC AND SETS (Semester 3)
Students will gather a very clear concept of set theory and its various properties.
Students will learn different logical approaches.
GE-Algebra (Semester 3)
Students will be able to calculate nth roots of unity and apply D’Moivre’s theorem.
Students will acquire knowledge on the theory of equations and it’s applications.
Students will be able to solve various inequalities and apply them on different problems.
Students will have a clear concept on functions, relations, well-ordering principle, division algorithm, principle of induction and their applications.
Students will be able to determine the rank of a matrix and its application on solving systems of linear equations.
Students will acquire knowledge on eigen values and eigen vectors.
Students will be acquainted with linear transformations and related problems.
MTMH-HCC-VIII (Semester 4)
Students will be able to solve problems on calculus of several variables.
Students will be able to calculate double and triple integrals.
Students will gather knowledge on vector analysis and its various applications.
MTMH-HCC-IX (Semester 4)
Students will acquire knowledge on ring theory.
Students will have a clear knowledge on vector spaces and its applications.
Students will be able to calculate problems on linear transformations.
MTMH-HCC-X (Semester 4)
Students will have deeper knowledge on metric spaces, specially on continuous mapping, compactness, connectedness, homeomorphism and its applications.
Students will learn complex analysis and its applications.
SEC II (Semester 4)
Students will acquire knowledge on different concepts of graph theory and its applications.
Students will learn to solve Travelling salesman’s problems.
Students will be eligible to write Dijkstra’s Algorithm, Warshall Algorithm.
GE-DE and Vector Calculus (Semester 4)
Students will acquire knowledge on solving linear homogeneous and non-homogeneous equations of higher order with constant co-efficient, Wronskian, method of undetermined co-efficient, method of variation of parameters.
Students will learn basic theory of linear systems in normal form, two equations in two unknown functions.
Students will be able to solve the power series solution of a differential equation about an ordinary and regular singular point.
Students will gather knowledge on how to apply vector triple product, vector calculus and vector integration.
MTMH-HCC-XI (Semester 5)
Students will be eligible to explain automorphism of groups and solve related problems.
Students will know about Characteristic subgroups, Commutator subgroups and their properties.
Students will know about the direct product of groups and can solve related problems.
Students will acquire knowledge on group action and can apply it to solve various problems on group theory.
Students will be eligible to write class equations of various groups.
Students will be eligible to explain and solve problems on Sylow Theorems.
MTMH-HCC-XII (Semester 5)
Students will be eligible to write algorithms, can calculate convergence and different types of errors of a given function.
Students will be eligible to solve Transcendental and polynomial equations by different methods.
Students will be able to solve systems of linear algebraic equations by different methods.
Students will be capable of solving problems by applying Lagrange’s and Newton’s interpolation formula, Finite difference operator, Numerical differentiation based on interpolation methods and finite difference methods.
Students will be eligible in solving numerical integration by various rules.
Students will be able to solve ordinary differential equations by method of successive approximation, Euler’s method, Runge - Kutta methods of orders two and four.
MTMH DSE-I:Linear Programming (Semester 5)
Students will be able to formulate LPP and can solve LPP by graphical method, simplex method, two-phase method, Big-M method.
Students will be able to explain Duality theory, can formulate dual problems and will have a clear concept on economic interpolation of the dual.
Students will be eligible in formulating and solving Transportation problems and Assignment problems.
Students will be able to formulate and solve two person zero sum game, graphical solution of game theory, linear programming solution of games.
MTMH DSE-II:Number Theory (Semester 5)
Students will have concepts on Gaussian integers, Euclidean algorithm, various concepts on gcd, consequences of unique prime factorization and can able to solve Diophantine equations.
Students will be able to solve problems on congruence arithmetic and learn related theorems.
MTMH-HCC-XIII (Semester 6)
Students will gather knowledge on polynomial ring, prime ideal, maximal ideal, principle ideal, irreducible and prime elements, Eisenstein criterion, unique factorization domains, Euclidean domains, Divisibility in integral domains and can solve related problems.
Students will be able to solve problems on dual space, dual basis, double dual, transpose of a linear transformation and its inverse matrix in the dual basis.
Students will be capable of solving problems on annihilators, eigen space of linear operator, the minimal polynomial for a linear operator, Diagonalizability, invariant subspaces, Cayley-Hamilton theorem, canonical forms.
Students will gather knowledge on inner product spaces and its various results and applications.
Students will be eligible in explaining Self-adjoint operator, Normal operator, Orthogonal projections and Spectral theorem.
MTMH-HCC-XIV (Semester 6)
Students will be able to explain what are partial differential equations, construct it, solve it and give geometrical interpretation of first order equations.
Students will be able to derive heat equation, wave equation, wave equation, Laplace equation; can classify second order linear equation as hyperbolic, parabolic or elliptic; can reduce second order linear equation to canonical form.
Students will be able to solve Cauchy problem of an infinite string, Initial boundary value problem, semi- infinite string with a fixed end as well as with a free end, equations non homogeneous boundary conditions, vibrating string problem, heat conduction problem.
Students will be eligible in solving problems on central force, constrained motion, varying mass, tangent and normal components of acceleration, modeling ballistic and planetary motion: Kepler’s second law.
MATH DSE-III :Point Set Topology (Semester 6)
Students will be eligible in explaining countable and uncountable sets, Schroeder - Bernstein Theorem, Cantor’s Theorem, Cardinal numbers and cardinal arithmetic, Continuum Hypothesis, Zorn’s lemma, Axiom of Choice, Well – ordered sets, Hausdorff’s maximal principle, Ordinal numbers.
Students will be able to define topological spaces, can give examples of topological spaces, and will have the knowledge on basic concepts on topological spaces with special emphasis on Product topology, Quotient topology, Metric topology, Baire-Category theorem.
Students will gather knowledge on Connectedness, Compact spaces and its various applications.
MATH DSE – IV : Theory of Equations (Semester 6)
Students will be able to represent polynomials graphically, calculate maximum and minimum values of a polynomial, find the nature of roots by applying Descarte’s rule of signs, solve problems on relation between roots and coefficients of equations.
Students will be eligible in solving problems on symmetric functions of roots, Transformation of equations, solution of reciprocal and binomial equations, algebraic solution of the cubic and biquadratic equations.
Students will be capable of applying Sturm’s theorem, Newton’s theorem.
COURSE OUTCOME (PROGRAMME COURSE)
DSC1(SEMESTER 1):
Eligible for finding Arc length of a curve, area of the region bounded by a given curve, Surface area and Volume of revolution by a curve about a given axis, techniques of sketching conics.
Eligible for derivation of reduction formulae of some special functions.
Eligible for calculating, application of Leibnitz rule and L’Hospital’s rule in business, economics and life sciences.
Eligible in various concepts and applications of two and three dimensions geometry.
Eligible for acquiring the knowledge about differential equations and its real life application.
DSC2(SEMESTER 2):
Students will be able to calculate nth roots of unity and apply D’Moivre’s theorem.
Students will acquire knowledge on the theory of equations and its applications.
Students will be able to solve various inequalities and apply them on different problems.
Students will have a clear concept on functions, relations, well-ordering principle, division algorithm, principle of induction and their applications.
Students will be able to determine the rank of a matrix and its application on solving systems of linear equations.
Students will acquire knowledge on eigen values and eigen vectors.
Students will acquire the knowledge about linear transformations and solving its related problems.
DSC3(SEMESTER 3):
Students will gather an elaborate knowledge on real number systems with special emphasis on completeness property of R, Archimedean property, density of rational numbers in R, Bolzano-Weierstrass theorem , Heine-Borel theorem.
Students will be able to understand the sequence of real numbers and its different properties.
Skill of determining convergence of infinite series of real numbers will be developed.
MATHPSEC-Logic and Sets(SEMESTER 3):
Students will gather a very clear concept of set theory and its various properties.
Students will learn different logical approaches.
DSC4(SEMESTER 4):
Students will acquire knowledge on solving linear homogeneous and non-homogeneous equations of higher order with constant co-efficient, Wronskian, method of undetermined co-efficient, method of variation of parameters.
Students will learn basic theory of linear systems in normal form, two equations in two unknown functions.
Students will be able to solve the power series solution of a differential equation about an ordinary and regular singular point.
Students will gather knowledge on how to apply vector triple product, vector calculus and vector integration.
MATHPSEC-Theory of Equations (SEMESTER 4):
Students will be able to represent polynomials graphically, calculate maximum and minimum values of a polynomial, find the nature of roots by applying Descarte’s rule of signs, solve problems on relation between roots and coefficients of equations.
Students will be eligible in solving problems on symmetric functions of roots, Transformation of equations, solution of reciprocal and binomial equations, algebraic solution of the cubic and biquadratic equations.
Students will be capable of applying Sturm’s theorem, Newton’s theorem.
DSE1-Group Theory and Linear Algebra(SEMESTER 5):
Students will be able to define group and can give examples of groups, specially permutation group, symmetries of a square, dihedral group, quaternion group.
Students will also learn different elementary properties of group theory.
Students will be able to describe subgroup, cyclic group,coests and normal subgroups.
Students will be able to define vector spaces, subspaces, quotient spaces, basis and dimension of subspaces and can solve related problems.
Students will be capable of solving various problems on linear transformations.
MATHPSEC-Probability and Statistics (SEMESTER 5):
Students will be able to define the definition of probability using the concepts of random experiment, sample space and can solve related problems.
Students will be able to define one and two dimensional distribution functions, density functions using random variables and can solve various related problems.
Students will be able to define one and two expectations, moment generating function, correlation coefficients, joint density functions, calculation of covariance, linear regression using joint random variables and can solve various related problems.
Students will be able to gather knowledge about Chebyshev’s inequality, weak and strong law of large number, central limit theorem and can solve various related problems.
DSE2-Linear Programming Problems(SEMESTER 6):
Students will be able to formulate LPP and can solve LPP by graphical method, simplex method, two-phase method, Big-M method.
Students will be able to explain Duality theory, can formulate dual problems and will have a clear concept on economic interpolation of the dual.
Students will be eligible in formulating and solving Transportation problems and Assignment problems.
Students will be able to formulate and solve two person zero sum game, graphical solution of game theory, linear programming solution of games.
MATHPSEC-Graph Theory (SEMESTER 6):
Students will acquire knowledge on different concepts of graph theory and its applications.
Students will learn to solve Travelling salesman’s problems.
Students will be eligible to write Dijkstra’s Algorithm, Warshall Algorithm.
2019-2022
Sl. No. |
Name |
Contact No. |
Current Status |
|
|---|---|---|---|---|
1 |
Akash Debnath |
6295833694 |
... |
|
2 |
Anindita Sarkar |
8348626602 |
.... |
|
3 |
Ankush Mitra |
8250170082 |
... |
|
4 |
Avishek Dhar |
6296512749, 7364070071 |
Medical Representative (MR) Course |
|
5 |
Darpan Roy |
6297828149 |
M.Sc., University of North Bengal |
|
6 |
Moloy Das |
7478814534 |
M.Sc., University of North Bengal |
|
7 |
Pankaj Saha |
6294386866 |
M.Sc., University of North Bengal |
|
8 |
Paritosh Roy |
9064899362 |
... |
|
9 |
Pulak Debnath |
6295699080 |
... |
|
10 |
Rajarshi Sarkar |
7001778906 |
M.Sc., IIT Madras |
|
11 |
Rick Bhattacharya |
9593157904 |
... |
|
12 |
Sandhya Roy |
7029612083 |
M.Sc., University of North Bengal |
|
13 |
Sanjita Roy |
8101534133 |
B.Ed. |
|
14 |
Sankalpa Barman |
9382473216 |
M.Sc., Darjeeling Hill University |
|
15 |
Sayan Majumder |
8515920866 |
PO GDS |
|
16 |
Sourav Roy |
6297514467 |
... |
|
17 |
Souvik Barman |
8918006194 |
M.Sc., University of North Bengal |
|
18 |
Sukdeb Mandal |
8583054232 |
... |
|
19 |
Suman Gope |
9734052111 |
M.Sc., NBU |
|
20 |
Suravi Das |
8372854583 |
Joint M.Sc. Ph.D., IIT Bhubaneswar |
2018-2021
Sl. No. |
Name |
Contact No. |
Current Status |
|
|---|---|---|---|---|
1 |
Ahidul Alam |
6296231008 |
B.Ed. |
|
2 |
Arpita Barman |
7797223238 |
B.Ed. |
|
3 |
Arup Roy |
6295770797 |
B.Ed. |
|
4 |
Azimul Hoque |
8327637790 |
B.Ed. |
|
5 |
Balaram Mandal |
8436402311 |
M.Sc., IIT Kanpur |
|
6 |
Chelshe Sarkar |
7407735855 |
B.Ed. |
|
7 |
Dhruba Barman |
8538814223 |
... |
|
8 |
Kaberi Barman |
8250658253 |
B.Ed. |
|
9 |
Kalyan Roy |
8334043563 |
B.Ed. |
|
10 |
Kanak Roy |
6296025379 |
B.Ed. |
|
11 |
Manoj Kumar Roy |
6295799106, 8653267280 |
B.Ed. |
|
12 |
Rabindra Nath Roy |
9382870813 |
B.Ed. |
|
13 |
Rabiprakash Sha |
7384765348 |
M.Sc., NIT Warangle |
|
14 |
Rahul Dev Barman |
6294644217 |
B.Ed. |
|
15 |
Raju Paul |
7318727946 |
B.Ed. |
|
16 |
Sabarna Roy |
8391919665 |
... |
|
17 |
Selim Alam |
9593629775 |
... |
|
18 |
Shobhan Roy |
9002861113 |
B.Ed. |
|
19 |
Subhodeep Roy |
7063539297 |
M.Sc., NBU |
|
20 |
Sulochana Roy |
9732640669 |
B.Ed. |
|
21 |
Tirthankar Sarkar |
8350089207 |
B.Ed. |
2nd Semester(Honours)
Sl. No. |
College Roll No. |
Name |
Contact No. |
|
|---|---|---|---|---|
1 |
3220002 |
Md. Ashif Ansari |
9064572059 |
|
2 |
3220004 |
Dilip Barman |
9883130266 |
|
3 |
3220005 |
Partha Protim Das Barman |
|
|
4 |
3220007 |
Prince Das |
9749727953 |
|
5 |
3220008 |
Tuhin Roy |
7318617229 |
|
6 |
3220009 |
Ranjan Roy |
|
|
7 |
3220010 |
Babu Barman |
|
|
8 |
3220013 |
Mangal Deep Das |
9883649523 |
|
9 |
3220018 |
Kalyani Roy |
|
|
10 |
3220020 |
Adnan Ali Miah |
7602629481 |
|
11 |
3220022 |
Rabindranath Sarkar |
9883496804 |
|
12 |
3220023 |
Deep Saha |
9339656141 |
|
13 |
3220024 |
Surojit Bhowmik |
9832188820 |
|
14 |
3220025 |
Biplab Roy |
8972283964 |
|
15 |
3220026 |
Firoj Alam |
9883417271 |
|
16 |
3220032 |
Prabal Mohanta |
8167887227 |
|
17 |
3220036 |
Basudev Sarkar |
9832762538 |
|
18 |
3220041 |
Sarifuzzaman Islam |
7427968033 |
|
19 |
3220046 |
Koushik Roy Patwary |
|
|
20 |
3220047 |
Debasis Barman |
9832808635 |
|
21 |
3220048 |
Sourav Roy |
|
|
22 |
3220050 |
Rishika Das |
|
|
23 |
3220051 |
Samiran Roy Sarkar |
|
|
24 |
3220063 |
Partha Roy |
8167468848 |
|
25 |
3220064 |
Debashish Roy |
9832462868 |
|
26 |
3220071 |
Ujjwal Ray |
7908105049 |
|
27 |
3220079 |
Dipayan Das |
6294737227 |
|
28 |
3220098 |
Abhijit Roy |
8167899681 |
|
29 |
3220102 |
Asim Barman |
|
|
30 |
3220108 |
Debojit Roy |
629719712 |
4th Semester(Honours)
Sl. No. |
College Roll No. |
Name |
Contact No. |
|
|---|---|---|---|---|
1 |
1202100-93675 |
Hiranmay Modak |
8145824875 |
|
2 |
1202100-93774 |
Kalyan Roy |
9933780433 |
|
3 |
1202100-93956 |
Rekha Roy |
9832472407 |
|
4 |
1202100-91881 |
Madhab Roy |
8016242218 |
|
5 |
1202100-94860 |
Akash Bhattyacharjee |
8509195455 |
|
6 |
1202100-94884 |
Pritam Biswas |
6296349213 |
|
7 |
1202100-91451 |
Satyabrata Roy |
7318900579 |
|
8 |
1202100-91797 |
Subham Barman |
9832946589 |
|
9 |
1202100-96104 |
Biman Saha |
8617655138 |
|
10 |
1202100-92376 |
Puja Roy |
8944965530 |
|
11 |
1202100-94642 |
Tanmay Baidya |
9064945776 |
|
12 |
1202100-93875 |
Parthib Roy |
8350031180 |
|
13 |
1202100-94474 |
Parthib Deb |
9641549636 |
|
14 |
1202100-92055 |
Himanshu Barman |
7001868753 |
|
15 |
1202100-96892 |
Subhamay Sarkar |
9883681894 |
|
16 |
1202100-96963 |
Riya Dey |
6296843641 |
|
17 |
1202100-94624 |
Debarati Dey |
9749045280 |
6th Semester(Honours)
Sl. No. |
College Roll No. |
Name |
Contact No. |
|
|---|---|---|---|---|
1 |
202000-95355 |
Rupamay Biswas |
8391985716 |
|
2 |
202000-90569 |
Shoumik Biswas |
7872290086 |
|
3 |
202000-93255 |
Santu Ray |
9679801530 |
|
4 |
202000-95014 |
Kailashpati Mandal |
6295103587 |
|
5 |
202000-92848 |
Adwiti Barman |
9635634938 |
|
6 |
202000-93557 |
Subham Dam |
9832990365 |
|
7 |
202000-94236 |
Debomay Saha |
6296365403 |
|
8 |
202000-91457 |
Arjun Barman |
7550991938 |
|
9 |
202000-95472 |
Somnath Sarkar |
6295836338 |
|
10 |
202000-95492 |
Ketaki Roy |
9430083719 |
|
11 |
202000-95623 |
Mowni Roy |
8509374829 |
|
12 |
202000-95582 |
Bodhisatwa Roy |
9932248217 |
|
13 |
202000-95570 |
Samrat Dey |
9641768115 |
Sukanta Mahavidyalaya
Department of Mathematics
Students Progression from July, 2017 to June, 2022
| Sl. No. | Name | Year of Passing | Admitted To | Course | JAM/NET/SET/GATE | Current Status | Present Institute/Department |
| 1 | Bapan Ali Miah | 2017 | University of North Bengal | M.Sc | NET (2020),SET (2022) | Ph. D Pursuing | NIT Silchar |
| 2 | Abhisekh Mallick | 2018 | University of North Bengal | M.Sc | NET (2022) | Ph. D Pursuing | University of North Bengal |
| 3 | Prosanta Roy | 2018 | University of North Bengal | M.Sc | --- | ---- | ---- |
| 4 | Arindam Roy | 2018 | --- | --- | --- | Service | W.B. EXISE Dept. |
| 5 | Koushik Sarkar | 2018 | --- | --- | --- | Service | Rail NTPC, Good Instructor |
| 6 | Gayn Bahadur Chetri | 2018 | --- | --- | --- | Service | Teacher of a Private School |
| 7 | Abhijit Adhikary | 2018 | --- | --- | --- | Service | SI of Police |
| 8 | Ajoy Roy | 2018 | --- | --- | --- | Service | Rail, Group D |
| 9 | Pinaj Roy | 2019 | NSOU | M.Sc | --- | --- | --- |
| 10 | Pitun Saha | 2019 | NSOU | M.Sc | --- | --- | --- |
| 11 | Tithi Sarkar | 2019 | NIT Durgapur | M.Sc | JAM (2019) | --- | --- |
| 12 | Pronoy Roy | 2020 | University of North Bengal | M.Sc | --- | --- | --- |
| 13 | Biswajit Mandal | 2020 | Raiganj University | M.Sc | --- | --- | --- |
| 14 | Subhodeep Roy | 2021 | University of North Bengal | M.Sc | --- | --- | --- |
| 15 | Balaram Mandal | 2021 | IIT, Kanpur | M.Sc | JAM (2021) | --- | --- |
| 16 | Rabiprakash Sha | 2021 | NIT Warangal | M.Sc. | JAM (2022) | --- | --- |
| 17 | Sandhya Roy | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 18 | Avishek Dhar | 2022 | --- | Medical Representative (MR) Course | --- | --- | --- |
| 19 | Darpan Roy | 2022 | University of North Bengal | M.Sc | --- | --- | ---- |
| 20 | Suravi Das | 2022 | IIT Bhubaneswar | M.Sc integrated Ph.D | JAM (2022) | --- | --- |
| 21 | Pankaj Saha | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 22 | Rajarshi Sarkar | 2022 | IIT Madras | M.Sc | JAM (2022) | --- | --- |
| 23 | Moloy Das | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 23 | Suman Gope | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 24 | Sukdeb Mandal | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 25 | Sankalpa Barman | 2022 | Darjeeling Hill University | M.Sc | --- | --- | --- |
Sukanta Mahavidyalaya
Department of Mathematics
Students Achievement from July, 2017 to June, 2022
| Sl. No. | Name | Year of Passing | Admitted To | Course | JAM/NET/SET/GATE | Current Status | Present Institute/Department |
| 1 | Bapan Ali Miah | 2017 | University of North Bengal | M.Sc | NET (2020),SET (2022) | Ph. D Pursuing | NIT Silchar |
| 2 | Abhisekh Mallick | 2018 | University of North Bengal | M.Sc | NET (2022) | Ph. D Pursuing | University of North Bengal |
| 3 | Prosanta Roy | 2018 | University of North Bengal | M.Sc | --- | ---- | ---- |
| 4 | Arindam Roy | 2018 | --- | --- | --- | Service | W.B. EXISE Dept. |
| 5 | Koushik Sarkar | 2018 | --- | --- | --- | Service | Rail NTPC, Good Instructor |
| 6 | Gayn Bahadur Chetri | 2018 | --- | --- | --- | Service | Teacher of a Private School |
| 7 | Abhijit Adhikary | 2018 | --- | --- | --- | Service | SI of Police |
| 8 | Ajoy Roy | 2018 | --- | --- | --- | Service | Rail, Group D |
| 9 | Pinaj Roy | 2019 | NSOU | M.Sc | --- | --- | --- |
| 10 | Pitun Saha | 2019 | NSOU | M.Sc | --- | --- | --- |
| 11 | Tithi Sarkar | 2019 | NIT Durgapur | M.Sc | JAM (2019) | --- | --- |
| 12 | Pronoy Roy | 2020 | University of North Bengal | M.Sc | --- | --- | --- |
| 13 | Biswajit Mandal | 2020 | Raiganj University | M.Sc | --- | --- | --- |
| 14 | Subhodeep Roy | 2021 | University of North Bengal | M.Sc | --- | --- | --- |
| 15 | Balaram Mandal | 2021 | IIT, Kanpur | M.Sc | JAM (2021) | --- | --- |
| 16 | Rabiprakash Sha | 2021 | NIT Warangal | M.Sc. | JAM (2022) | --- | --- |
| 17 | Sandhya Roy | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 18 | Avishek Dhar | 2022 | --- | Medical Representative (MR) Course | --- | --- | --- |
| 19 | Darpan Roy | 2022 | University of North Bengal | M.Sc | --- | --- | ---- |
| 20 | Suravi Das | 2022 | IIT Bhubaneswar | M.Sc integrated Ph.D | JAM (2022) | --- | --- |
| 21 | Pankaj Saha | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 22 | Rajarshi Sarkar | 2022 | IIT Madras | M.Sc | JAM (2022) | --- | --- |
| 23 | Moloy Das | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 23 | Suman Gope | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 24 | Sukdeb Mandal | 2022 | University of North Bengal | M.Sc | --- | --- | --- |
| 25 | Sankalpa Barman | 2022 | Darjeeling Hill University | M.Sc | --- | --- | --- |
| COURSE | CLASS | PAPERS |
|---|---|---|
| Honours | Semester-I | CC-1 CC-2 |
| Semester-II | CC-3 CC-4 | |
| Semester-III | CC-5 CC-6 CC-7 SEC(H)-1 | |
| Semester-IV | CC-8 CC-9 CC-10 SEC(H)-2 | |
| Semester-V | CC-11 CC-12 DSE(H)-1 DSE(H)-2 | |
| Semester-VI | CC-13 CC-14 DSE(H)-3 DSE(H)-4 | |
| Programme | Semester-I | DSC-1 |
| Semester-II | DSC-2 | |
| Semester-III | DSC-3 SEC(P)-1 | |
| Semester-IV | DSC-4 SEC(P)-2 | |
| Semester-V | DSE(P)-1 SEC(P)-5 | |
| Semester-VI | DSE(P)-2 SEC(P)-4 | |
| GE | Semester-I | GE-1 |
| Semester-II | GE-2 | |
| Semester-III | GE-3 | |
| Semester-IV | GE-4 |
Department of Mathematics Sukanta Mahavidyalaya
SPECIAL LECTURE ON ‘NECESSITY AND IMPORTANCE OF NUMERICAL ANALYSIS’
Dated: 18th November, 2022


CELEBRATION OF TEACHERS’ DAY 2022
Date: 6th September, 2022

STUDENTS’ FAREWELL PROGRAMME 2022
Date: 13th August, 2022


EDUCATIONAL TOUR 2022
Dated: 13th June, 2022


SPECIAL LECTURE ON ‘A JOURNEY FROM METRIC SPACES TO TOPOLOGICAL SPACES’
Dated: 19th April, 2022


CELEBRATION OF NATIONAL SCIENCE DAY
DATED: 28TH February, 2022


RESULT ANALYSIS Department of Mathematics
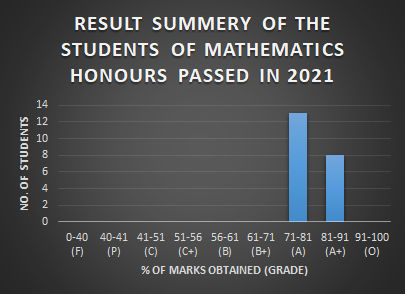
RESULT ANALYSIS OF MATHEMATICS HONOURS STUDENTS PASSED IN 2021
GRADE |
F |
P |
C |
C+ |
B |
B+ |
A |
A+ |
O |
Total No. of Students |
|---|---|---|---|---|---|---|---|---|---|---|
| % Obtained | 0-40 | 40-41 | 41-51 | 51-56 | 56-61 | 61-71 | 71-81 | 81-91 | 91-100 | |
No. of Student |
0 |
0 |
0 |
0 |
0 |
0 |
13 |
8 |
0 |
21 |
RESULT ANALYSIS OF MATHEMATICS HONOURS STUDENTS PASSED IN 2022
GRADE |
F |
P |
C |
C+ |
B |
B+ |
A |
A+ |
O |
Total No. of Students |
|---|---|---|---|---|---|---|---|---|---|---|
| % Obtained | 0-40 | 40-41 | 41-51 | 51-56 | 56-61 | 61-71 | 71-81 | 81-91 | 91-100 | |
No. of Student |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
13 |
0 |
20 |

Google form links for submission of Answer Sripts
Department of Mathematics
Sukanta Mahavidyalaya
The students must create a single PDF file for answer scripts of each paper maintaining the
following guidelines:
1) Each page of the answer scripts should contain the Page sequence (Number).
2) File format should be in PDF format only.
3) File size should not exceed 10 MB.
4) File Name should be in the following format-University Roll No & Paper Name.
GOOGLE FORM LINKS
For CBCS System: https://forms.gle/TCHvfrQW6ghPTabA6
For further details or any doubt please contact to the Department of Mathematics, Sukanta
Mahavidyalaya.